Аннотация: Рассмотрена методика численного моделирования стационарного течения вязкой и идеальной жидкости при обучении основам вычислительной физики. Предложены программы на Pascal.

Обучение основам компьютерного моделирования предполагает решение задач механики сплошных сред численными методами [2]. Рассмотрим течение вязкой жидкости, которое инвариантно по отношению к переносам в направлении движения (течение жидкости в трубе, обтекание бесконечно длинного корабля и т.д.). Для его расчета следует определить скорости в сечении, перпендикулярном направлению течения (оси z), то есть решить уравнение: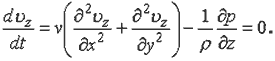

Если dp/dz=0, то в конечных разностях получаем:

Решение конкретной задачи требует правильного задания граничных условий [1]: слои вязкой жидкости, прилегающие к поверхности твердого тела, имеют одинаковую с ним скорость. Если жидкость имеет свободную поверхность, то скорость частиц этой поверхности равна скорости частиц, расположенных слоем ниже. На рис. 1 представлены результаты расчета обтекания длинного корпуса корабля, течения в трубе при разности давлений, движения жидкости в трубе в случае, когда вдоль ее оси протягивается нить.

uses crt, graph; const n= 90; m=58; h=1; dt=0.02;     {ПР-1}
var  ii,jj,kk,i,j,DV, MV, EC : integer; 
vv, v: array[1..N, 1..M] of real;
procedure Gr_usl; {---- Граничные условия ----}
begin for i:=1 to N do for j:=1 to M do v[i,j]:=vv[i,j]; 
for i:=2 to N-1 do for j:=2 to M-1 do begin 
if (j<5)and(abs(5-i)<5) then v[i,j]:=0;
if (j<40)and(abs(i-50)<1+20*sqr(cos(j/25))) then v[i,j]:=300; 
end; 
for i:=1 to N do v[i,M]:=0; 
for j:=1 to M do begin v[1,j]:=0; v[N,j]:=0; end; end;
procedure Raschet; {---- Расчет скорости ----}
begin vv[i,j]:=v[i,j]+(v[i,j+1]-2*v[i,j]+v[i,j-1])*dt/(h*h)
+(v[i+1,j]-2*v[i,j]+v[i-1,j])*dt/(h*h); end;
procedure Draw;{---- Вывод на экран ----}
begin setcolor(round(v[i,j]/40)); if v[i,j]<1 then setcolor(9);
{if round(v[i,j]/60) grOK then Halt(1);
Repeat Gr_usl; for i:=1 to N-1 do for j:=2 to M-1 do Raschet;
Gr_usl; for jj:=2 to M-1 do for ii:=1 to N-1 do 
begin i:=N+1-ii; j:=M+1-jj; Raschet; end;
for i:=1 to N do vv[i,1]:=vv[i,2]; kk:=kk+1;
if kk/30=round(kk/30) then 
                 for i:=2 to N-1 do for j:=2 to M-1 do Draw;
until KeyPressed; CloseGraph;
END.

Рассмотрим установившееся потенциальное течение идеальной жидкости в трубе прямоугольного сечения. Такое течение является плоским, характеризуется потенциалом скорости и функцией тока, для них выполняются уравнения Лапласа:

Семейство линий равного потенциала скорости ортогонально совокупности линий тока. Для них можно записать:

Значения функции тока находят с помощью конечно–разностного уравнения (считаем, что Δ x=Δ y):

Подобный метод используется при решении уравнения теплопроводности, а также при расчете электрических полей [1, 2]. В программе перебираются узлы сетки, при этом пересчитываются значения функции тока и через каждые 10 итераций выводится на экран (рис.2). Граничные условия задаются в процедуре Gran usl. Значения у верхней и нижней поверхности трубы, включая выступы, устанавливается равными 200 и –200, а на концах трубы они изменяются пропорционально координате. В точках, где находятся препятствие, функция тока равна 0.

uses crt, graph; const n=140; m=50;	                 {ПР-2}
var i,ii,j,jj,k, DV, MV, EC : integer; 
psi: array[1..N, 1..M] of real;
procedure Raschet; {---- Расчет потенциала ----}
begin 
 psi[i,j]:=(psi[i+1,j]+psi[i-1,j]+psi[i,j+1]+psi[i,j-1])/4; 
end;
procedure Gran_usl; {---- Граничные условия ----}
begin for i:=1 to N do begin psi[i,2]:=-200; psi[i,M-1]:=200;
psi[i,1]:=-200; psi[i,M]:=200; end;
for j:=1 to M do begin 
    psi[N-1,j]:=-204+8*j; psi[N,j]:=-204+8*j; end;
for j:=1 to 25 do begin 
    psi[2,j]:=-204+16*j; psi[N-1,j]:=-204+8*j;
psi[1,j]:=-204+16*j; psi[N,j]:=-204+8*j; end;
for i:=1 to N do for j:=1 to M do 
if (j>25)and((i-60)*(i-60)+(j-25)*(j-25)<200) then psi[i,j]:=0;
for i:=1 to N do for j:=1 to M do 
if (abs(j-25)<15)and(abs(i-110)<5) then psi[i,j]:=0;
for i:=1 to N do 
    for j:=1 to M do if (j>25)and(i<30) then psi[i,j]:=200; end;
procedure Draw; {---- Вывод на экран ----}
begin setcolor(round((psi[i,j]+200)/20));
if ((j>25)and((i-60)*(i-60)+(j-25)*(j-25)<200)) 
or ((j>25)and(i<30))or((abs(j-25)<15)and(abs(i-110)<5)) 
                                      then setcolor(0);
rectangle(i*4+50,j*4,i*4+53,j*4+3); end;
BEGIN DV:=Detect; InitGraph(DV,MV,'c:\bp\bgi');
EC:=GraphResult; if EC <> grOK then Halt(1);
Repeat  inc(k); Gran_usl; 
for i:=2 to N-1 do for j:=2 to M-1 do Raschet;
Gran_usl; for jj:=2 to M-1 do
for ii:=2 to N-1 do begin i:=N+1-ii; j:=M+1-jj; Raschet; end;
if k/10=round(k/10) then begin cleardevice;
for i:=2 to N-1 do for j:=2 to M-1 do Draw; end;
until KeyPressed; CloseGraph;
END.

1. Тихонов А.Н., Самарский А.А. Уравнения математической физики. –– Москва: Наука, 1966. –– 724 c.

2. Сайт: http://maier-rv.glazov.net (электронный ресурс).

Майер Р.В. Расчет течения жидкости на компьютере / Физика в школе и вузе. Международный сборник научных статей. Выпуск 6. --- С.Петербург: Изд-во РГПУ, 2007. --- С. 57--60.